√無料でダウンロード！ 1/ルート1-x^2 積分 848890-1/ルート1-x^2 積分

Dec 10, 12 · 不定積分の問題です。 ∮ 1/√(x^21) dx インテグラル ルートx2乗足す1 分の1 こちらが解けません(インテグラルの記号が見つからないので記号はこちらでお許し下さい) 私は ∮ (x^21)^1/2 dx =√(x^21)/x C としたのですが間違えみたいです。Apr 03, 18 · 上野竜生です。√(x 2 a 2)の積分を丁寧に解説しようとすると長くなったのでラスボス前の中ボス程度の1/√(x 2 a 2)は別ページにわけることにしました。 ラスボスについてはこちらをご覧ください。 今回考える積分前回学習した√(1x 2)の積分と同じように考えましょう。ルートの中身が，もし2乗の形であれば，ルートがうまく外れてくれますね。 (4x 2)を 2 に置換 する方法を考えます。

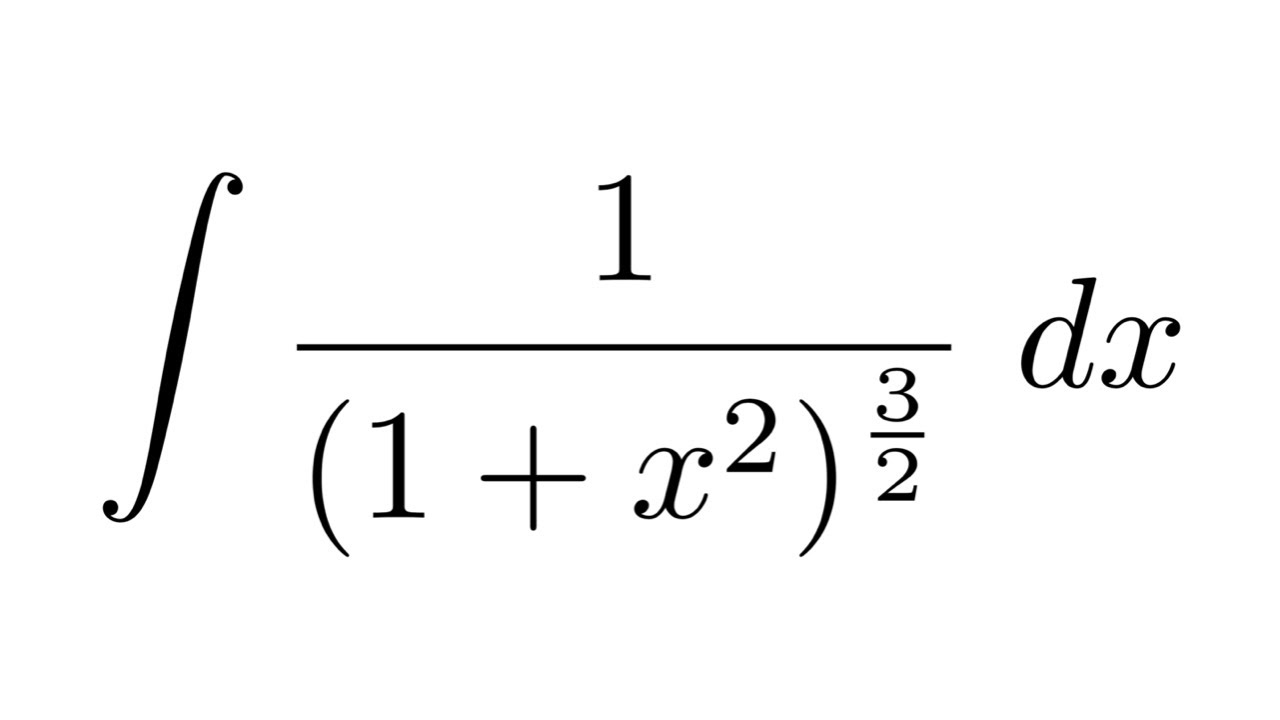
Integral Of 1 1 X 2 3 2 Substitution Youtube

1/ルート1-x^2 積分

1/ルート1-x^2 積分-定積分の置換積分法では， (1) 被積分関数 (2) 積分変数 (3) 積分区間 の3箇所を書き換える． ※定積分は，積分区間の下端・上端の値を代入すると定数になるので，不定積分の置換積分法とは異なり，変数を元に戻す必要はない． 例 2x−1=t とおくXで積分しようと思うと，xと√(1x)の積になっている上，√(1x)は合成関数になっているので，とても積分しにくいですね。 そこで， ルートの中身をシンプルな式に置き換えて積分 するのが置換積分法

置換積分法とは 5つのステップから分かる置換積分のやり方とコツ アタリマエ

本時の目標 置換積分により， √x a を含む無理関数の不定積分を求めることができる。 1 √1 − x2 を含む不定積分を求めることができる。 u = x √1 x2 の置き換えにより， ∫ 1 √1 x2 dx を求めることができる。 部分積分を用いて， ∫√1 − x2dx ， ∫1 積分練習問題解答 1 つぎの不定積分を計算せよ。 (1) ∫ x 1 x2 2x5 dx d dx (x2 2x5) = 2(x1)だから x 1 x2 2x5 x1 x2 2x5 2 x2 2x5 と変形して，y = x2 2x5 とおくとdy = 2(x1)dx だから ∫ x1 x2 2x5 dx = ∫ dy 2y = logjyjC = 1 2 log(x2 2x5)C一方，後半の積分はx 22x5 = (x1) 4 なので，y = (x1)/2 と書くとMay 18,  · この記事では、特定の 1/√1x^2の積分 について 置換積分を2回 行う方法で解説します。 また、 置換積分を1回でのみ解ける簡略的な方法 についても解説しています。 最後には、例題もありますので、例題を見ながら理解していただくのもおすすめです

1 x2 の積分にSin 1x が出て来たのには扇型 の面積が関わっていました。これに対応して次で定義される双曲線関数： sinhx = ex x 2 coshx = x e x 2 は自明な関係式：cosh2 x sinh2 x = 1 が示す通り、(x;y) = (sinht;cosht) で双曲線 y2 x2 = 1 の（上半分の）パラメータ表示になっています。 ∫ 1 p 1x2∫1 0 dx 1x4 = 1 2 ∫1 1 dx 1x4 = 1 2 ∫ C(R!1) dz 1z4 = ˇ 2 p (149) 122 フーリエ積分 任意の波形を三角関数の和に分解するフーリエ変換に必要となる積分 ∫1 1 f(x)cos(sx)dx;1−x2 であるので, 部分積分すると, ∫ arcsinxdx = xarcsinx− ∫ x √ 1−x2 dx = xarcsinx √ 1−x2 例題17 次の関数を積分せよ (1) exsinx, (2) 1 (x2 a)n (a̸= 0 ,n̸= 1) 略解例(1) は高校でよくやっているだろう (2) も同じ考えでできる In= ∫ 1 (x2 a)n dx とおく 分子を(x2 a−x2

Sep 22, 19 · 積分では sin ⁡ 2 \sin^2 sin2 とか cos ⁡ 2 \cos^2 cos2 がきたら半角の公式だから、ここはすぐに反応できるようにね。 半角の公式 cos ⁡ 2 x = 1 cos ⁡ 2 x 2 \displaystyle \cos^2 x=\frac {1\cos 2x} {2} cos2 x = 21cos2x1B'nn tan −1 xB'nn C ※この形の不定積分を関数として表すためには逆三角関数を必要とするため，高校では扱われないのが普通．ただし，同じ形でも 定積分 は数値の差＝定数となるから，この形の定積分は高校の範囲に入る． (16) 分母が数種類の2次式の積になっている場合 ∫wn sxp(ax2bxc)m(dx2exf)nnnnnnnnnnnnnnnnnnnnn dx (a,d ≠0,m,n=2,3,) 部分分数分解Dec 17,  · ルートの中に2乗を含む積分 (1) \ \int f\left(\sqrt{a^{2}x^{2}}\right)dx=a\int f\left(a\cos t\right)\cos tdt\cnd{x=a\sin t} \ (1)2

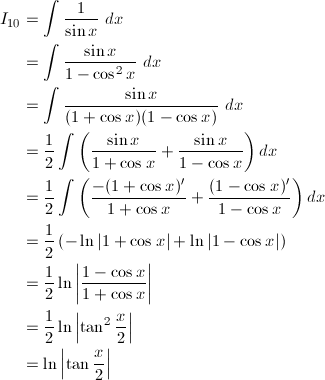
不定積分選 グラフ付き 数学自由研究

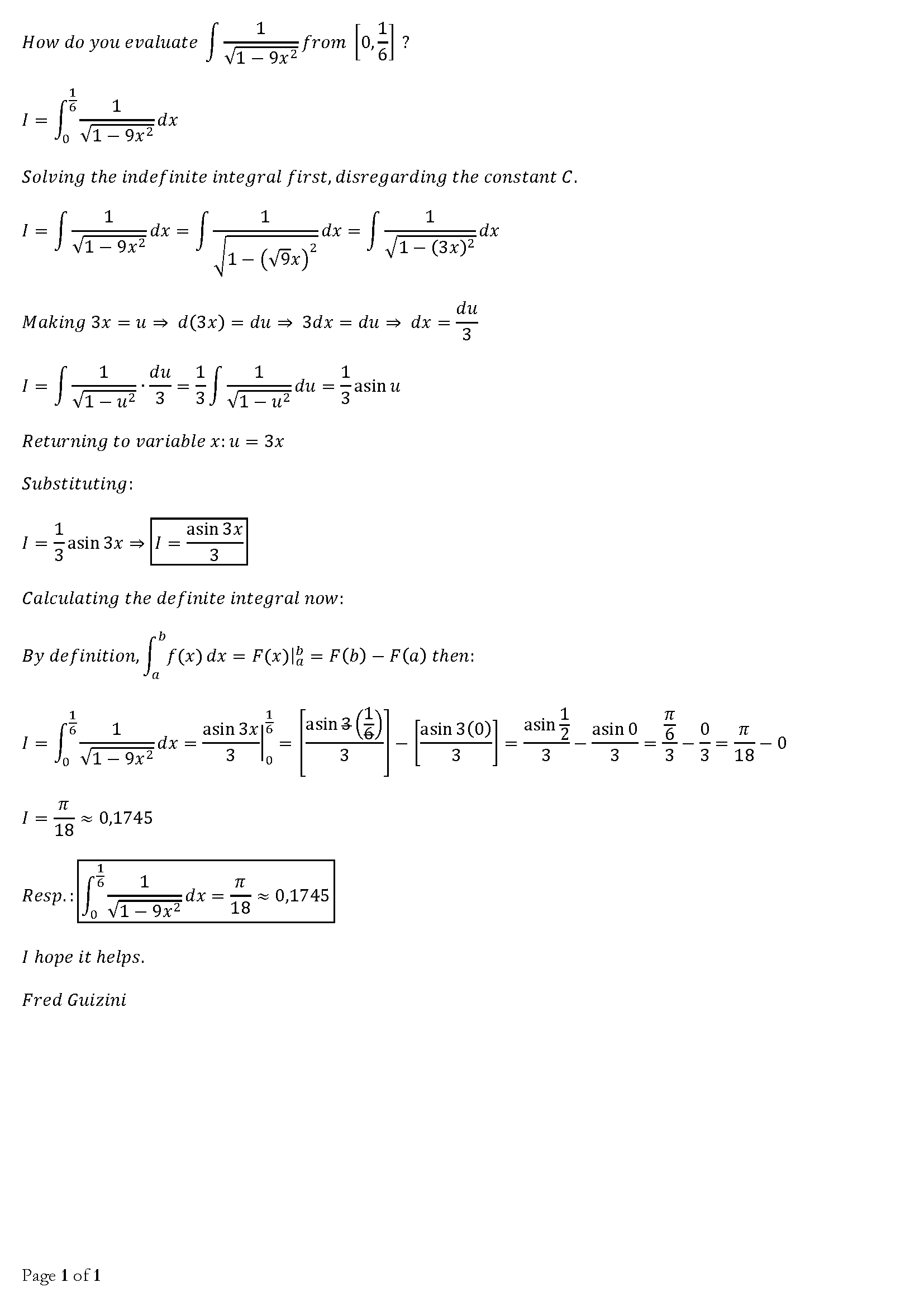
How Do You Evaluate Int1 Sqrt 1 9x 2 Dx From 0 1 6 Socratic

Nov 16, 18 · 次の不定積分を計算しなさい。 ∫ 1 √x2 1 dx ∫ 1 x 2 1 d x 「 その1 」と似ていますが、分母が x√x2 1 x x 2 1 から √x2 1 x 2 1 に変わっています。 小さな違いですが、計算はまた大きく変わってきます。 ここでは、「その1」の後半で見た、 tan tan に置き換える方法から見ていきましょう。 x = tant x = tan ⁡ t (− π 2 < t < π 2) ( − π 2 < t < π 2) と置きます。 tant tanNov 15, 18 · ルートを丸ごと置換する方法 次の不定積分を計算しなさい。 ∫ 1 x√x2 1 dx ∫ 1 x x 2 1 d x 分母があまりきれいな形ではないので、分母を何か別の文字で置きたいですね。 いろいろ候補が考えられますが、ここでは、 u = √x2 1 u = x 2 1 としてみましょう。 右辺を微分すると 1 2 ⋅(x2 1)−1 2 ⋅(x2 1)′ = x √x2 1 1 2 ⋅ ( x 2 1) − 1 2 ⋅ ( x 2 1) ′ = x x 2 1 となりJul 24, 18 · 方針1：分母分子に1cosxをかける 最も思いつきやすい方法ですが上の＜重要＞を使った方針2のほうが楽です。 また方針2のほうが \sqrt {1\cos {x}} の積分などに応用するのが簡単なので実はあまりオススメではありません。 答え \displaystyle \int \frac {1} {1\cos {x

高校数学 定積分の置換積分 ３ 問題編 映像授業のtry It トライイット

積分 逆双曲線関数 何度も置換を乗り越えて No 049 衒学記鳥の日樹蝶

部分積分法 より． f ′ (x) = 1, g(x) = √a2 x2 f ′ ( x) = 1, g ( x) = √ a 2 − x 2 = x√a2 x2 − ∫a2 x2 − a2 √a2 x2 dx = x √ a 2 − x 2 − ∫ a 2 − x 2 − a 2 √ a 2 − x 2 d x = x√a2 x2 − ∫√a2 x2dx ∫ a2 √a2 x2dx = x √ a 2 − x 2 − ∫ √ a 2 − x 2 d x ∫ a 2 √ a 2 − x 2 d x = x√a2 − x2 − ∫√a2 − x2dx a2 sin − 1x aJul 16, 19 · \ \int^{1}_0 x \sqrt{1 x^2} \ dx \を積分しなさい。 (1) まともに置換積分 まずは普通に置換積分をしてみましょう。 \( t = \sqrt{1x^2} \) とします。すると、\( t^2 = 1 x^2 \) となり、\( 2t dt = 2x dx \) となるので、\( dx = \frac{t}{x} \) となります。Mar 06, 21 · ルートx^2a^2の積分計算の2通りの方法 レベル ★ 最難関大受験対策 積分 更新日時 公式1： ∫ d x x 2 a 2 = log ⁡ ( x x 2 a 2) \displaystyle\int \dfrac {dx} {\sqrt {x^2a^2}}=\log (x\sqrt {x^2a^2}) ∫ x2 a2

数3です 378の 2 で 1 X 1 Tとして計算することはできますか Clear

平方根内が２次式である関数の不定積分 身勝手な主張

Aug 24,  · 積分1/√1x^2の積分、1/ax^2の積分、2回の置換を行う この記事では、特定の1/√1x^2の積分について置換積分を2回行う方法で解説します。 また、置換積分を1回でのみ解ける簡略的な方法についても解説しています。X 1 dx = lnx 1 C (12) （C は積分定数） 112 n = 2 I2 = Z 1 x2 1 dx = arctanx C (13) （C は積分定数） 113 n = 3 I3 = Z 1 x3 1 dx (14)となりました．確かに の微分が被積分関数になっていますね． まとめ 覚えやすいように，他の積分と比較できるようにまとめておきます．いきなり書きますが，良い練習問題になると思います．まずは，右辺を に等しいと置いて， を求めるのです．ちなみに としておきます．

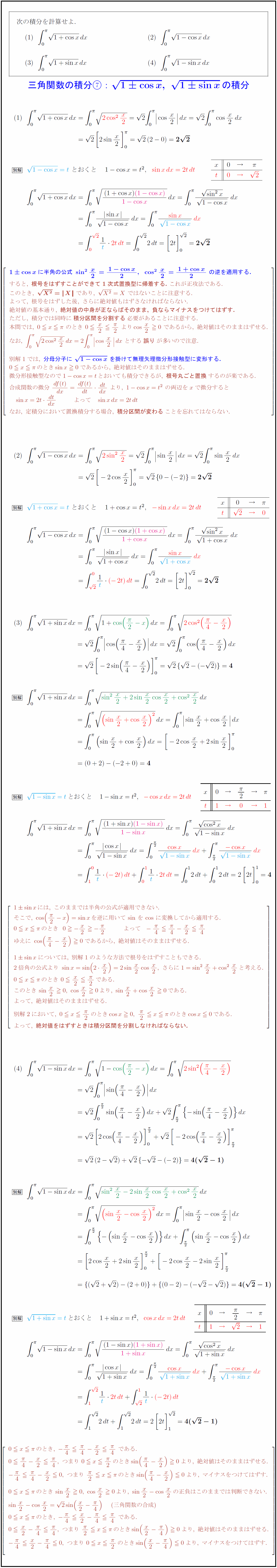
三角関数の積分 1 Cosx Dx 1 Sinx Dx 3つの解法 受験の月

数学 積分計算の型網羅part1 置換積分 理系ラボ

積分する関数を入力してください 変数 積分電卓 解析積分を用いて所与の変数に対する関数の不定積分 (アンチ導出)を計算する。 また、関数のグラフとその積分を描画することもできる。 計算された不定積分は、Cが任意の定数である関数F (x)Cのクラスに属することを覚えておいて下さい。 積分演算子は、構文解析を行い、積分規則を適用することで、最終結果を（補題11 と定理12）によりこの不定積分が計算できる． 注意 14 3 角関数の有理関数の不定積分は，この定理 1 3 によって必ず計算できるが，一 般にこの計算は複雑になることが多い．そのため，問題によっては別の変数変換を行った方Jul 25, 19 · 実際に2つの積分を計算します。 1つ目 ∫ − 1 − t 1 x 2 d x = − 1 x − 1 − t = − 1 1 t lim t → 0 1 t = ∞ となり、 ∫ − 1 − t 1 x 2 d x = ∞ ∫ t 1 1 x 2 d x = − 1 x t 1 = − 1 1 t lim t → 0 1 t = ∞ となり、 ∫ t 1 1 x 2 d x = ∞ となり、2つの広義積分はともに無限大に発散するので、 ∫ − 1 1 1 x 2 d x = ∞ となり、無限大に発散することがわかる。 （2つに分解した際に

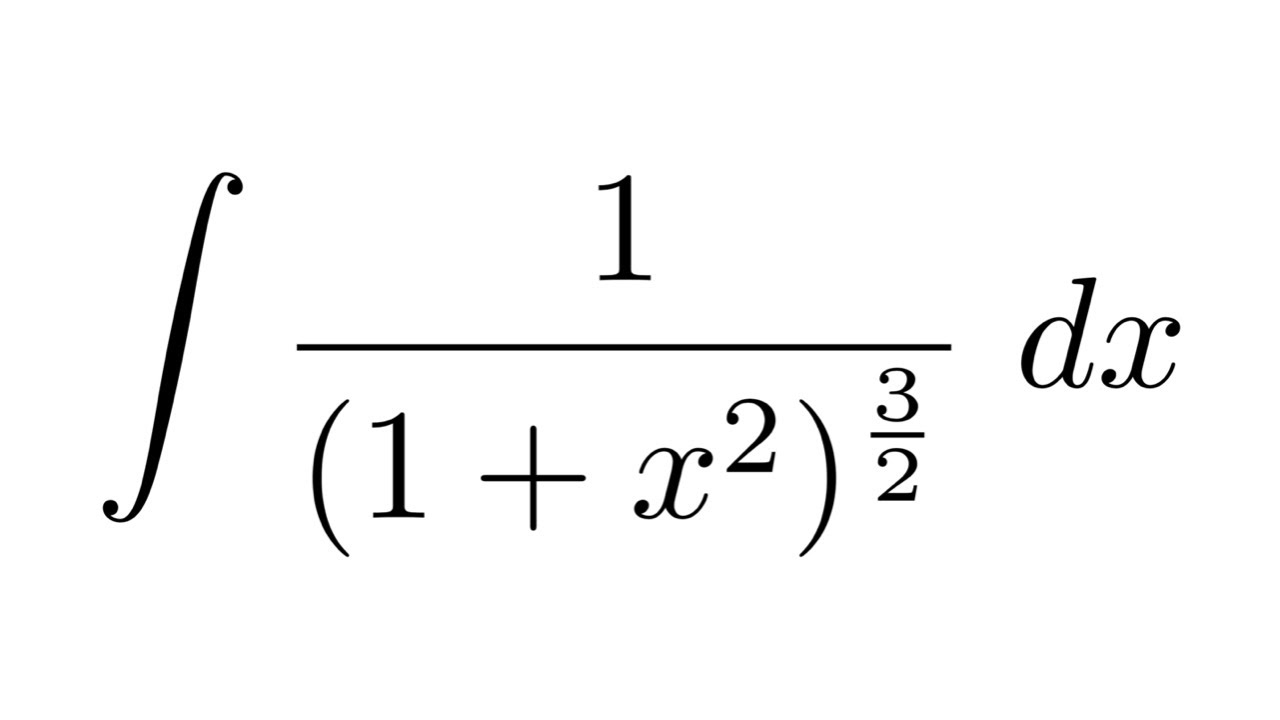
Integral Of 1 1 X 2 3 2 Substitution Youtube

1

Jun 12, 08 · ある演習問題で ∫1/√ (x^2A) という形が出てきて、それが解けずに解答を見たら、 ∫1/√ (x^2A) = logx√ (x^2A) という記述で、この積分の問題は済まされていました。 逆算すると、確かにそうなるのですが、なかなかこの形を直接考え出すのは、難しい(8) 部分積分を3回行って計算する I8 = Z x 3(e x)′dx = x e −3 Z x2exdx = x3ex −3 Z x2(ex)′dx = x3ex −3(x2ex − Z 2xexdx) = x3e x−3x2ex 6 Z xexdx = x3ex −3x2e 6(xex − Z exdx) = x3ex −3x2ex 6xex −6ex C (9) 1 1 x2 2x (1 x2)2 に注意すれば, 次のようになる I9 = Z x (−1 2(1 x2) dx = x −1 2(1 x2) − Z (−1不定積分を計算する： x^5 dxの積分 x^2 sin^3 x の積分 ∫e^t sin (5t) 基本項では表せない不定積分を計算する： e^ (t^2)の積分 1/sqrt (1u^4)を積分する 与えられた関数を含む積分の表を生成する： cos (u)を含む積分

置換積分の公式と例題 三角関数sin Tanを使ったパターンの解き方 アタリマエ

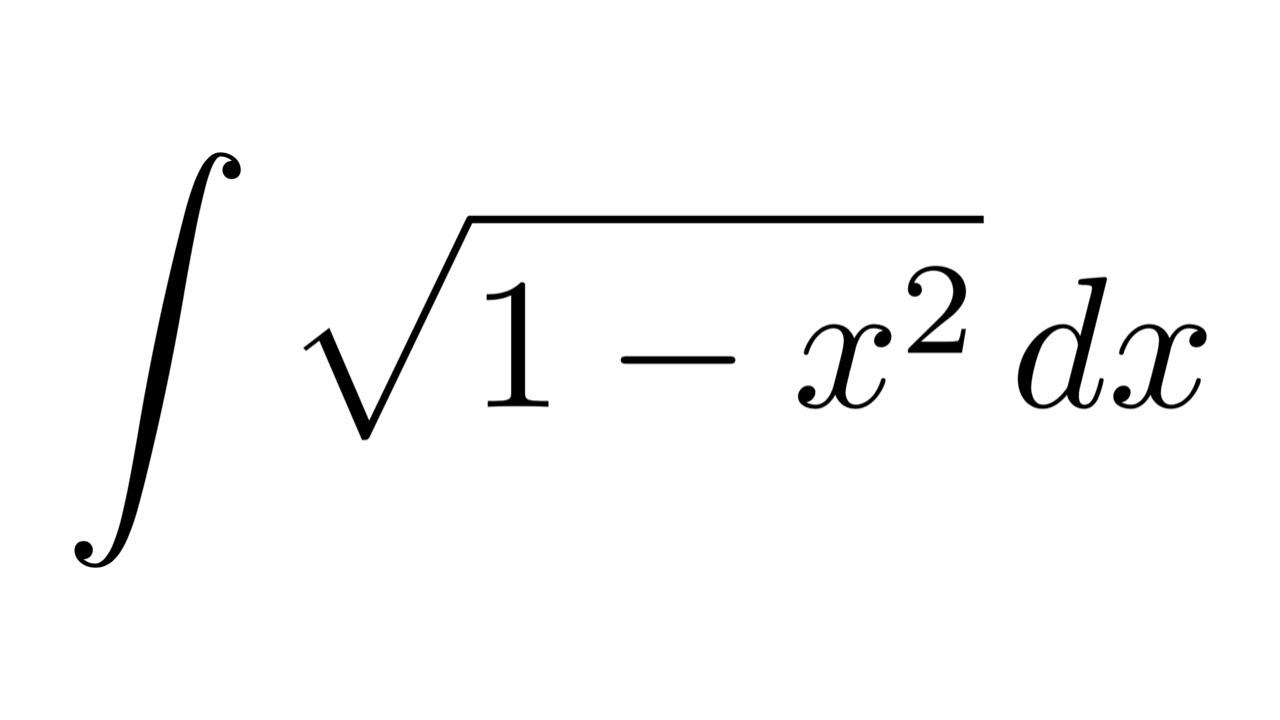
Integral Of 1 Sqrt 1 X 2 Substitution Youtube

Nov 18, 17 · 1/xのフーリエ変換 ※ただし、 での値は定義しない。 また、 は符号関数 数値計算による上式の確かめは 1/xのフーリエ変換 をご覧ください。 実軸上の積分は複素平面の上から近づいた値と下から近づいた値の平均をとって定めるとします。 すなわち積分 1/ (sin x )^2 ∫ 1 sin2x dx ∫ 1 sin 2 x d x （ cot x の微分 を参考） = ∫ sin2xcos2x sin2x dx = ∫ sin 2 x cos 2 x sin 2 x d x （∵ sin2xcos2x = 1 sin 2 x cos 2 x = 1 ） = ∫ −(cosx)′sinxcosx(sinx)′ sin2x dx = ∫ − ( cos x) ′ sin x cos x ( sin x) ′ sin 2 x d xFeb 16, 10 · √a^2x^2の不定積分がわかりません。わかる方いらっしゃいましたら回答お願いしますm(__)mその式のルートはどこまでかかっていますか?√a^2x^2 と書くと普通は (√a^2)x^2 (= a x^2) と解釈されますが, それでいいですか?

置換積分法とは 5つのステップから分かる置換積分のやり方とコツ アタリマエ

1

Jun 23, 15 · 1/√(x(1x)) 、範囲は(0,1)の定積分について質問です。 この積分は本来、arcsinの積分の形で広義積分するものらしいのですが、x=cos^2tと置いて広義積分してはいけないのでしょうか？微積分 導関数 積分 微積分電卓 行列計算機 数学の問題を入力 解 代数 三角法 統計 微積分 行列 変数 リスト \int{ 1 }d x/int/sqrt (x^21) dxをどう積分しますか？双曲線関数を用いたらcosh^2 tの積分まで行ったのですがここからどうしたらいいのか分かりません。

部分積分の解き方とコツ どっちを微分するか判断するポイントとは アタリマエ

数学問題 T Nakaの阿房ブログ

Jun 27,  · ルートの積分は最初に方針2を試そう！ それでダメなら方針3を試そう！ 方針1が使えそうだと気付いたら使ってみよう。 これでおおよそルートの積分は大丈夫のはずです。 最後に講義資料と積分ドリルの宣伝をのせて終わりとします。Jun 30, 09 · 置換 積分 を用いて解く。 √x2 a2 = t − x とおいて t の 積分 に書き換える *1 *2 。 この置き換えでは tをxの式で表すと t = x √x2 a2 xをtの式で表すと x = t2 − a2 2t ↑この式よりdxの変換は dx = t2 a2 2t2 dt √x2 a2 をtの式で表すと √x2 a2 = t2 a2 2t これらを代入してxの式をtの式に書き換える。 例題 ∫ dx √x2 a2 = ∫ 2t t2 a2t2 a2 2t2 dt = ∫dt t = ln(t) C = ln(x51 複素積分の定義 実数の積分は、区分求積法に基づいて定義される。 a x bの範囲で実関数f(x)を積分することを考える。このとき、積分区間を a = x0 < x1 < < xn 1 < xn = b とn個の区間に分割し、これを用いて ∫ b a f(x) lim n!1 ∑n i=1 f(^xi∆ xi ∆ xi xi xi 1) (64)

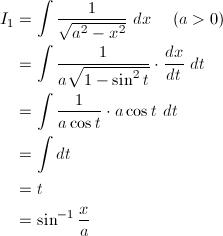
不定積分選 グラフ付き 数学自由研究

ルートx 2 A 2の積分計算の２通りの方法 高校数学の美しい物語

Dxdθnn =a cos θ → dx=a cos θ dθ ※ この変換は， x= cos θ とおいてもでき， √a2−x2 √nnnnni が分母にある場合でもできます． 右に続く→ →続き なお，次の形の定積分については， a 2 −x 2 =t とおく置換積分により，速攻で解くことができます． a∫ 0www x √a2−x2√nnnnni dx (a>0)X/√(1x^2) の積分 は高校の教科書レベルだ． 答えは， √(1x^2) えーっと，x=sin tとおけば dx=cos t dt だから 分子は x dx= sin t cos t dt 分母は √(1sin^2)=√(cos^2)=cos t で分子の cos と約分して， ∫ sin t dt となるから = cos t = √(cos^2 t) = √(1sin^2 t) = √(1x^2)広義積分 例 定積分 z 1 0 1 √ x dx を考える。これを次のように計算する のはそのままでは定義に反する： z 1 0 1 √ x dx = 2 √ x 1 0 = 2 理由 を定義する為の 和は発散し得る： aa aa aa aa aa aa aa aa aa aa aa a a a a a a a aa aa aa aa aa aa aa aa aa aa 1 x 微分積分・同演習b – p2/12

曲線の長さ ５ 逆双曲線関数が背景にある不定積分 怜悧玲瓏 高校数学を天空から俯瞰する

1 X 2 の積分を教えてください 模範回答と Yahoo 知恵袋

2 無理関数とは 無理関数 •「変数と定数の四則演算」および「根号（平方根や冪根）」 によって表される関数． 例 (x2 2) √ 2 − 3x, 1 √ x, x2 3 √ x2 1, • 根号の中に少なくとも1つの変数を含まなくてはならない 例 x2 3 √ 2 は無理関数ではない (2/14)微積分I 14 53 被積分関数e2x はf(u) = eu，u = 2x と分解すれば合成関数f(g(x)) とみ なせる．u′ = g′(x) = 2 であるので，問題の不定積分を以下のように変形し 置換積分できるようにする． ∫ e2xdx = 1 2 ∫ e2x 2dx 1 2 ∫ eudu 1 2 eu C 1 2 e2x C 上の計算では定理46 を素直に適用した．この適用のし

１ X 2 の積分ルート内を置換してやっていくのかと思いましたが部分積分を Yahoo 知恵袋

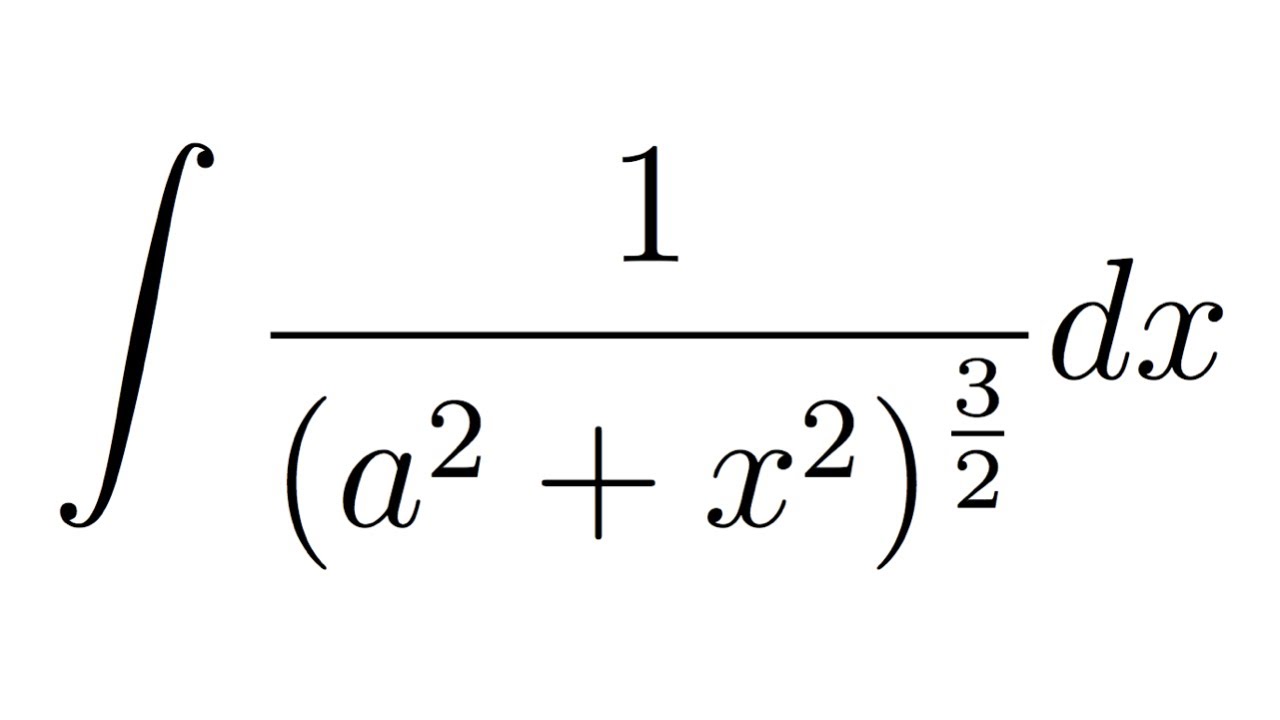
Integral Of 1 A 2 X 2 3 2 Substitution Youtube

1

分数関数の不定積分

Evaluate The Integral Of 1 A Bx2 Stumbling Robot

Int 2 2 X 3cos X 2 1 2 Sqrt 4 X 2 Dx

高校数学 特殊な置換をする不定積分 X A を含む不定積分 最高難度 と特殊な置換の根拠 受験の月

ガウス積分 Wikipedia

How To Integrate 4 X 2 1 2 Quora

ルートxの二乗 3分の1を微分しなさいという問題で私は画像のように Yahoo 知恵袋

平方根内が２次式である関数の不定積分 身勝手な主張

高校数学 特殊な置換をする定積分 A X を含む定積分はx Asin8とおけ 受験の月

1 X 2 A 2 Dxの計算 物理のかぎしっぽ

ルート X 2 1 を積分してください 答えにはlog絡んでます Peing 質問箱

Gaussian Integral Wikipedia

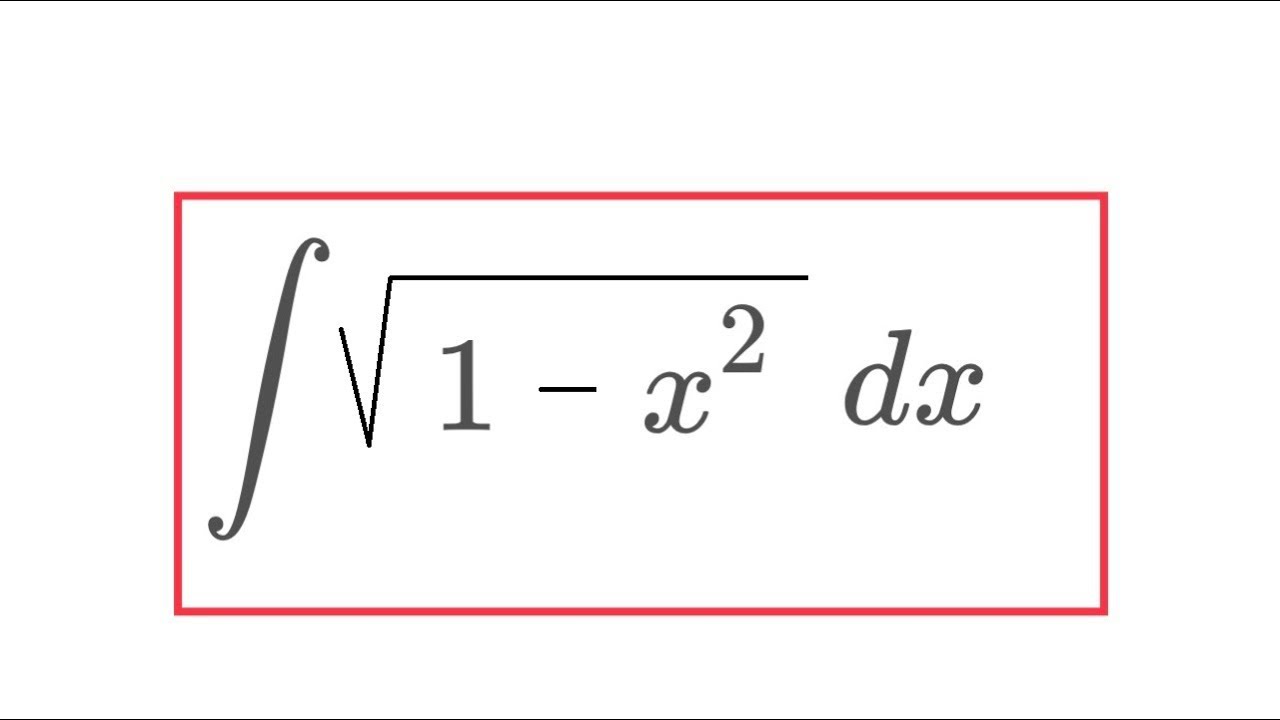
Integral Sqrt 1 X 2 Youtube

１ X 2 の積分ルート内を置換してやっていくのかと思いましたが部分積分を Yahoo 知恵袋

X 2 A 2 の積分 数学の偏差値を上げて合格を目指す

ヤマト やみょ ん٩ W و X 1 X 2 T で置くなら移項してルート消して 1 X 2 T X 2 整理して 1 T 2 2tx X T 2 1 2t から積分編集dx Dtの形にして解けばおけ ง W ว 今帰宅したからちょっとやってみるね W W

置換積分の公式と例題 三角関数sin Tanを使ったパターンの解き方 アタリマエ

積分 高校数学の美しい物語

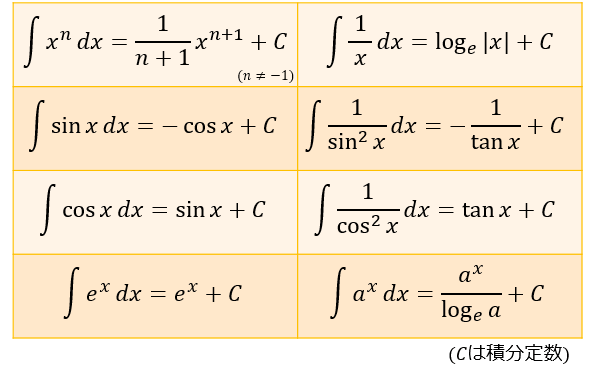
積分の公式一覧 アタリマエ

解析学基礎 基本的な積分 Wikibooks

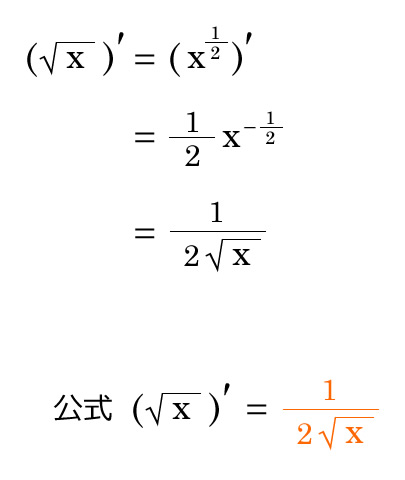
平方根の微分 優技録

高校数学 置換積分法 １ 問題編 映像授業のtry It トライイット

ルートx2乗 1は整数関数ですよね その場合一より優先して積分されるはずですが逆です Clear

高校数学 定積分の置換積分 ２ 問題編 映像授業のtry It トライイット

X 3 X 2 1 の不定積分 申し訳ありませんが 画像を作成しましたの 数学 教えて Goo

微分積分の授業でわからない問題があったので解説お願いしたいです まず Yahoo 知恵袋

How To Integrate 1 Sqrt X 2 1 Youtube

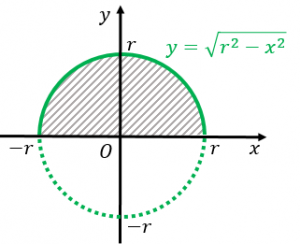
円の面積を積分で計算する２通りの方法 具体例で学ぶ数学

積分 置換積分 何をtとおく 数学の偏差値を上げて合格を目指す

X X分の１ ルート5の時 X X分の１の答えは何になります Yahoo 知恵袋

Y 1 X ２乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo

平方根内が２次式である関数の不定積分 身勝手な主張

What Is The Integration Of 1 Sinx 1 2 Quora

解析学基礎 基本的な積分 Wikibooks

不定積分の問題です この問題の解き方が分かりません 1 Yahoo 知恵袋

1

Gaussian Integral Wikipedia

平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス

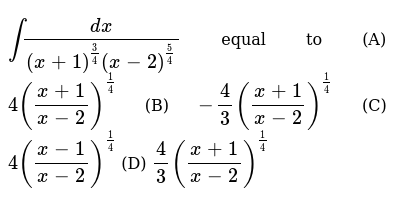
Int Dx X 1 3 4 X 2 5 4 Equal To A 4 X 1 X 2

高校数学 無理関数 Y X 1 X のグラフ 斜め楕円 受験の月

How To Integrate X 3cosx 2 1 2 Sqrt 4 X 2 Dx For The Interval Of 2 And 2 Quora

解析学基礎 基本的な積分 Wikibooks

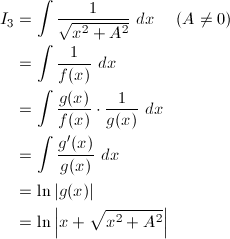
不定積分選 グラフ付き 数学自由研究

X 1 X 2dxの積分が解けません 置換積分で解くのはわかるんです Yahoo 知恵袋

解析学基礎 基本的な積分 Wikibooks

高校数学 定積分の置換積分 ３ 問題編 映像授業のtry It トライイット

基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート

How Do You Integrate 1 X 2 Sqrt 1 X 2 Socratic

合成関数とは 微分 積分の公式や証明 問題の解き方 受験辞典

X ルートx 2 1の積分教えてください ルートは 1ま Yahoo 知恵袋

How To Integrate 1 X 2 3 2 Quora

高校数学 定積分と面積 ２ 問題編 映像授業のtry It トライイット

基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート

Http Math Cs Kitami It Ac Jp Kouno Kougi Bi05a Kaisetu12 Pdf

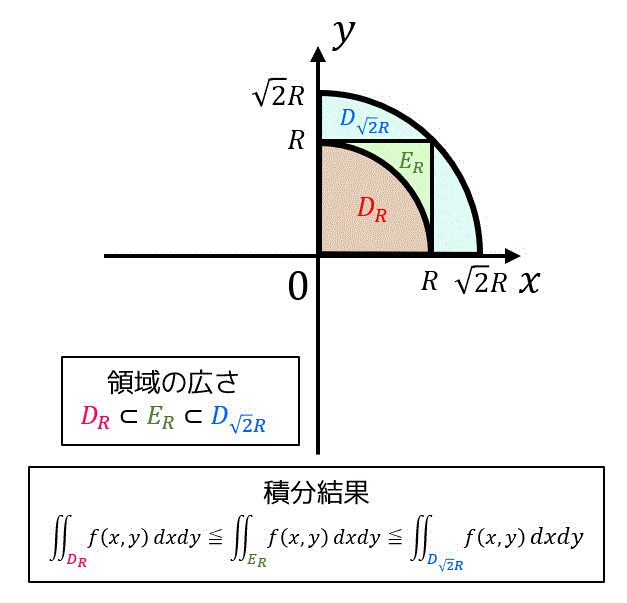
うさぎでもわかる解析 Part26 広義2重積分 ガウス積分 工業大学生ももやまのうさぎ塾

平方根の微分 優技録

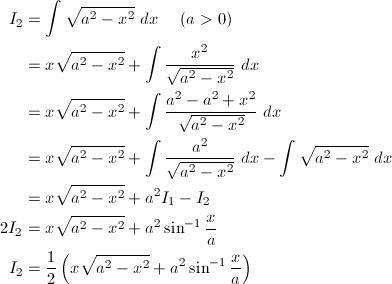
不定積分選 グラフ付き 数学自由研究

勉強 不定積分 X 2 1 Dx

積分 Sqrt 1 X 2 Integral Of Sqrt 1 X 2 Youtube

広義積分の極限を取るタイミングについてです Clear

置換積分法とは 5つのステップから分かる置換積分のやり方とコツ アタリマエ

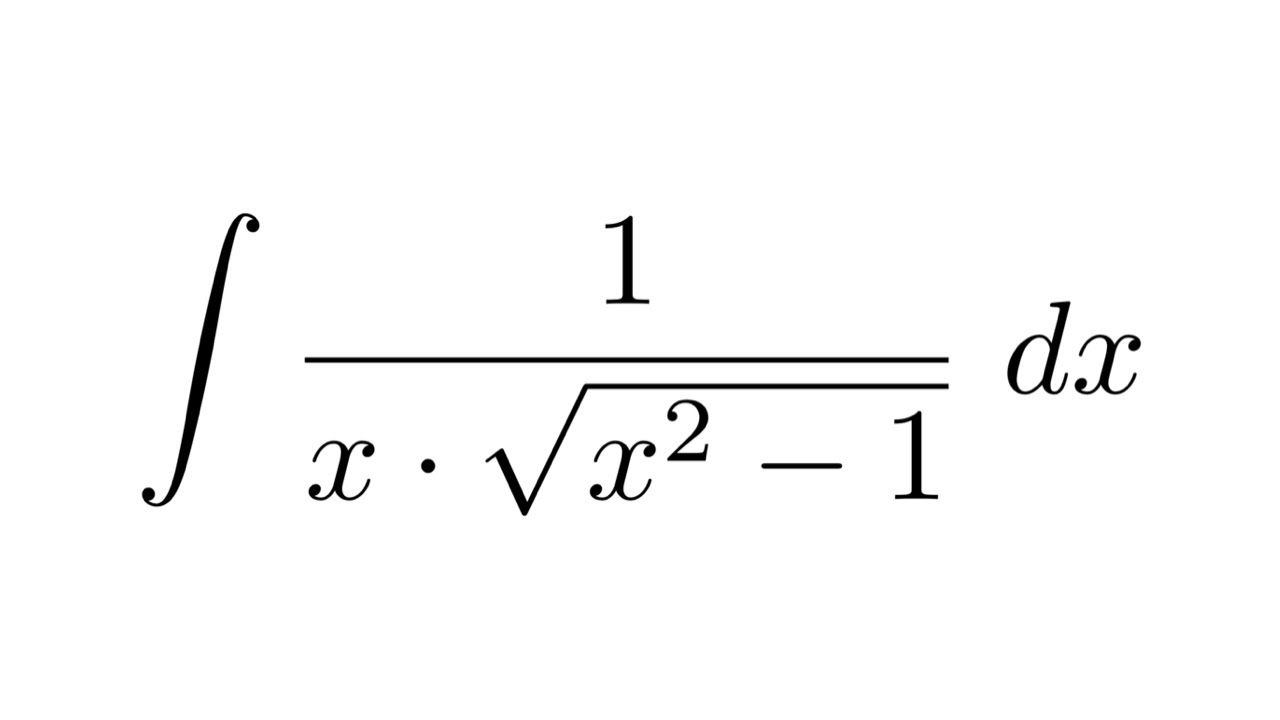
Method 1 Integral Of 1 X Sqrt X 2 1 Substitution Youtube

How To Integrate 1 X 2 1 2 Quora

1 X 2 A 2 Dxの計算 物理のかぎしっぽ

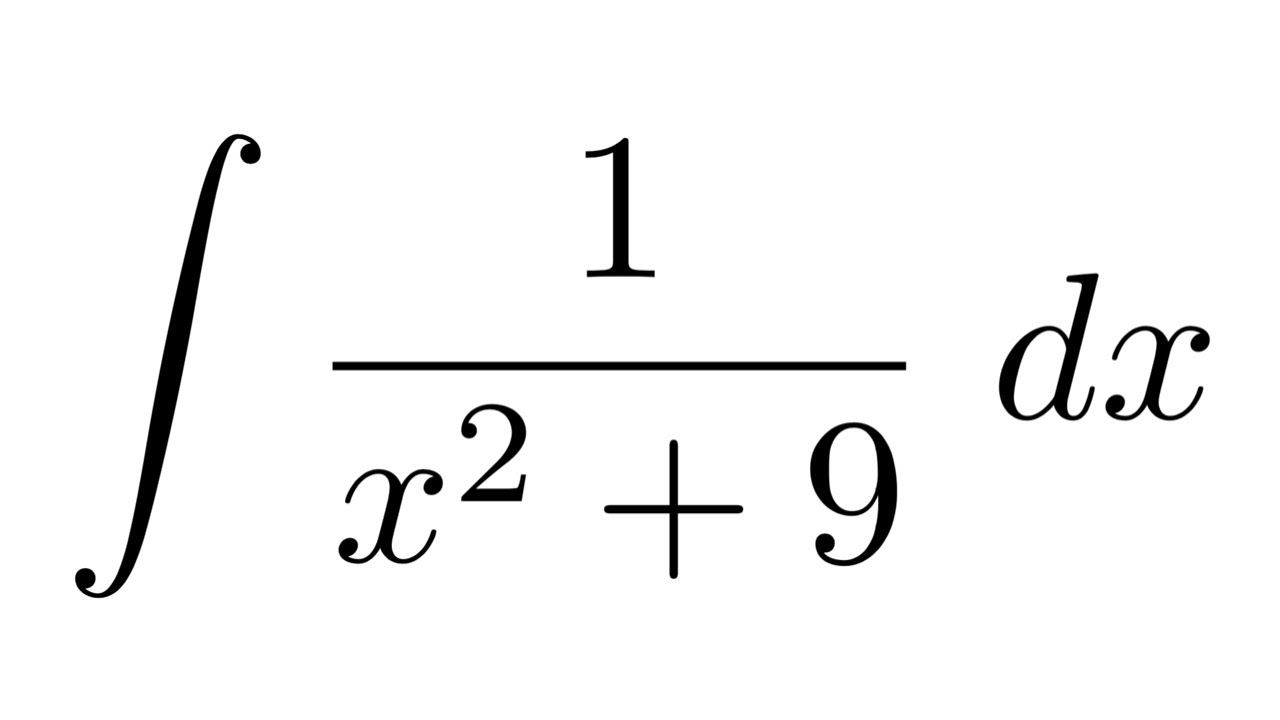
Integral Of 1 X 2 9 Substitution Youtube

高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月

でーすくん 綺麗な解法だと思います ੭ ᑦ ちなみに こういう複雑な根号は ルートを丸ごとuと置くと被積分関数から ルートがなくなって見通しがよくなる 機械的に解きやすくなる ことがあります 今回だったら1 1 U の形が出てくるのでu Tan8と

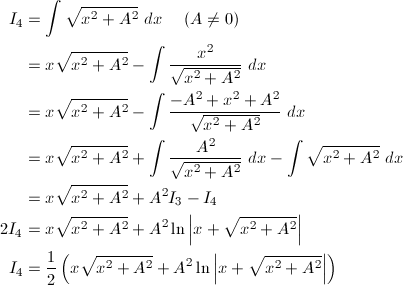
不定積分選 グラフ付き 数学自由研究

数 次の不定積分を求めよ 1 X X 2 Dx 2 Yahoo 知恵袋

Integral Of 1 Sqrt 1 X 2 Substitution Youtube

解析学基礎 基本的な積分 Wikibooks

不定積分ですが ルートと分数が混ざると急にやり方が分からなくなりま 高校 教えて Goo

分数関数の不定積分

Ex 7 4 2 Integrate 1 Root 1 4x2 Class 12 Ncert Ex 7 4

ルートの積分について Y X X 1 X 2 の曲線の長さを求める時に 曲線をl 数学 教えて Goo

Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C

積分の公式一覧 アタリマエ

置換積分の Dx の指導方法について 怜悧玲瓏 高校数学を天空から俯瞰する

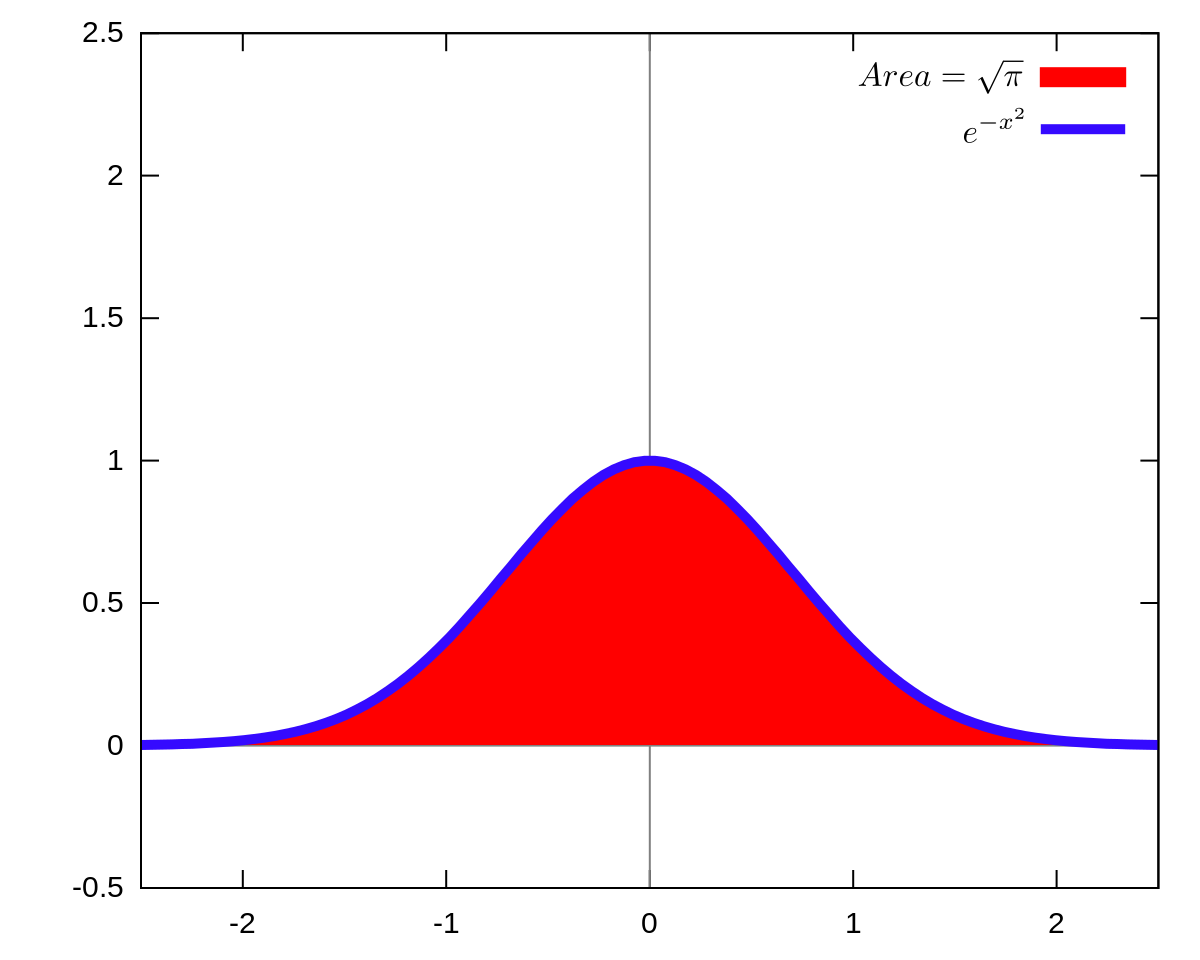
Gaussian Integral Wikipedia

高校数学 置換積分法 １ 問題編 映像授業のtry It トライイット

数iii 無理関数 1 X 2 型の積分 Sin に置きかえ Mm参考書

Incoming Term: 1/ルート1-x^2 積分,